Models of Learning

• Introduction

  1. Task description

• Reinforcement Learning

  1. Theory
     • Rescorla-Wagner
     • SoftMax
  2. Data plotting
  3. Simulation
     • Example participants
     • More participants
     • Explore Parameters
     • Grid Search
     • Marginal distributions
     • Summary values
  4. Real data
     • Fit the data
     • Statistical inference
  5. Review
     • Modelling how-to

• Bayesian Learning

  1. Coin tossing
     • Probability
     • Likelihood
     • Uncertainty
     • Learning
     • Review
  2. Bandit task
     • Updating
     • Transition function
     • Learning rate

Developed by
Jill O'Reilly
Hanneke den Ouden
-August 2015

Bayes' Theorem and sequential learning

Say that instead of revealing the sequence of coin tosses all at once, we do them one at a time.
How should the observer's beliefs about q evolve as each new coin toss in the sequence is observed?

We can model the observer's evolving beliefs using Bayes' Theorem.
Let the sequence of coin tosses be denoted y₁, y₂, y₃... y_i
Then:

p(q|y_1:i) ∝ p(y_i|q) p(q|y_1:i-1)

Where:

• p(q|y_1:i) is the posterior probability of some value of q given all the observed data on trials 1-i
• p(y_i|q) is the likelihood function for some value of q given most recent coin toss
• p(q|y_1:i-1) is the prior probability of some value of q given all the coin tosses up until the most recent one

Let's walk this through-

• On trial 1, we have no prior knowledge about the value of q, so the posterior probability of each candidate value of q is given by the likelihood function alone.
  
  • Say I observe a head on trial 1. What would be the likelihood that the true value of q is 0.8?
    (remember: q is the probability that the coin comes up heads)

    ?

    p(q|y₁)=p(y₁|q)=0.8

  • Now say I observe a tail on trial 1. What would be the likelihood that the true value of q is 0.8?

    ?

    p(q|y₁) = p(y₁|q) = (1-0.8) = 0.2

  • Can you work out what the likelihood function over all candidate values of q for 0 to 1 should look like, given that I observed a head ?

    ?

    It should be a straight line sloping up from
    

    (0,0) - i.e., p(heads|q=0) = 0 to
    (1,1) - i.e., p(heads|q=1) = 1
    

    

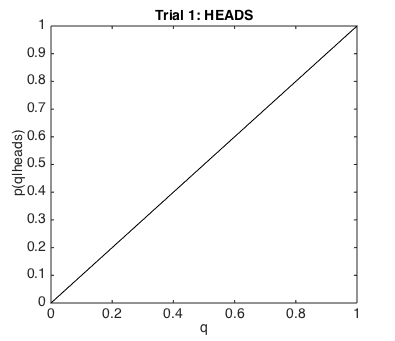
    Remember, q is the probability of the coin coming up heads!
    so if q was 0, it would be impossible to get a head!

  • Can you work out what the likelihood function over all candidate values of q for 0 to 1 should look like, given that I observed a tail ?

    ?

    It should be a straight line sloping down from
    

    (0,0) - i.e., p(tail|q=0) = 1 to
    (1,1) - i.e., p(tail|q=1) = 0
    

    

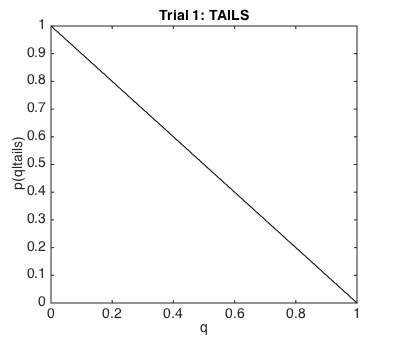
    Remember, q is the probability of the coin coming up heads!
    so if q was 1, the coin would always come up heads and it would be impossible to get a tail!

• On trial 2, we can again calculate the likelihood function p(q|y₂)=p(y₂|q), but we also want to take into account our prior knowledge p(q|y_1:i)=p(q|y₁) - ie the likelihood function from trial 1.
  • For a given candidate value of q, the posterior is p(q|y₂)*p(q|y₁).
    Say I observe the sequence HT. What is the posterior probability that q=0.6?

    ?

    p(q=0.6 | y₁ = H) = p(y₁ = H | q=0.6) = 0.6
    p(q=0.6 | y₂ = T) = p(y₂ = T | q=0.6) = 1 - 0.6 = 0.4
    p(q=0.6 | y₁ = H, y₂ = T) = p(y₁ = H | q=0.6)*p(y₂ = T | q=0.6) = 0.6 * 0.4 = 0.24
    

  • If we perform the calculations above for every candidate value of q between 0 and 1, we get a distribution that expresses the posterior probability of each value of q.
    Can you work out what this would look like for the sequences HH, TT and HT?

    ?

    

• On trial 3, we again have a likelihood function p(q|y₃)=p(y₃|q), and a prior.
  The prior p(q|y_1:i-1)=p(q|y_1:2) needs to capture information from trials 1 and 2. But the posterior from trial 2 is exactly that - when i=2, the posterior p(q|y_1:i)=p(q|y_1:2), the prior for trial 3.
  • Section 3 or the Matlab script UncertaintyTutorial1.m works out the posterior probability for each value of q after each of a series of coin tosses.
    Run this section of the script and have a look at how the posterior evolves

  ?

  

  • Try altering the sequence of coin tosses and observing how the posterior evolves then.
    In particular -
    • If you change the order of the Hs and Ts but not the number of each, does the posterior on the last trial change?
    • What if you increase the number of coin tosses but keep the proportion of Hs and Ts the same?
      How does the posterior on the last trial differ if you have 15 coin tosses instead of 5?
      What about the uncertainty?

►►►